
처음 코드트리를 들어갔는데, 마침 조별과제 이벤트를 하더라?
마침 DFS/BFS 기초부터 배울 수 있길래 이번에 정복?을 해보고자 한다.
1. Depth-First Search [약칭 DFS]란?
뭔가 되게 있어 보이지 않는가?
사전적 의미로는 " 맹목적 탐색방법의 하나로 탐색트리의 최근에 첨가된 노드를 선택하고, 이 노드에 적용 가능한 동작자 중 하나를 적용하여 트리에 다음 수준(level)의 한 개의 자식노드를 첨가하며, 첨가된 자식 노드가 목표노드일 때까지 앞의 자식 노드의 첨가 과정을 반복해 가는 방식이다."
라고 상당히 장황하게 적혀있는데..
우리는 우리 입맛대로, 손쉽게 이해해 보도록 하자.
그냥 한 길만 죽어라 파면서 남는 길이 없을 때까지 반복하는 거다.
2. DFS 이해를 위한 예시
2-1. DFS 이해 예시 #1
자.. 아래 사진과 같이 뚫린 지점이 여러 곳 있는 미로가 있다고 하자.
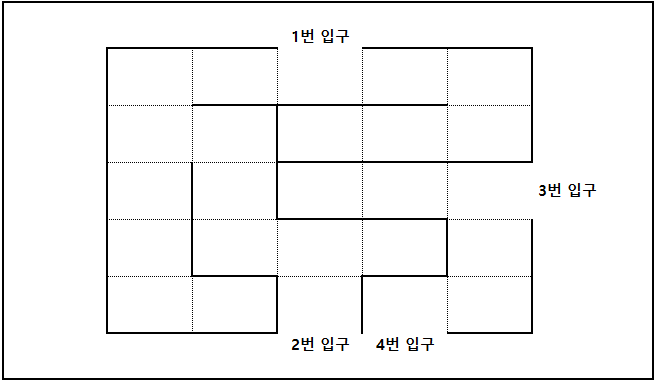
우리는 우선 하나의 길을 선택하고, "더 이상 갈 수 있는 길"이 없을 때까지 이동할 것이다.
"1번 입구"를 선택한 상태로 제일 먼저 만나는 길을 중심으로 이동한다고 하면, 아래 색칠 된 부분만큼 이동하게 된다.
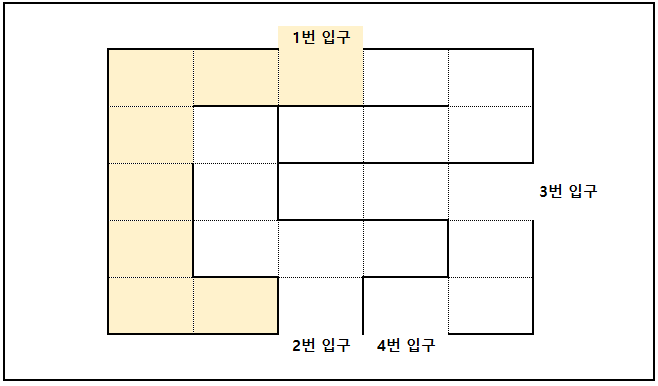
그럼 한 칸씩 다시 돌아오면서 연결된 다른 길이 있는지 확인한다.
돌아오는 와중에 연결된 길이 또 있으면 그 길이 막힐 때까지 이동한다.
그럼 아래 색칠 된 부분만큼 이동하게 된다.
조금 더 진한 색은 중복으로 이동된 부분으로 보자!
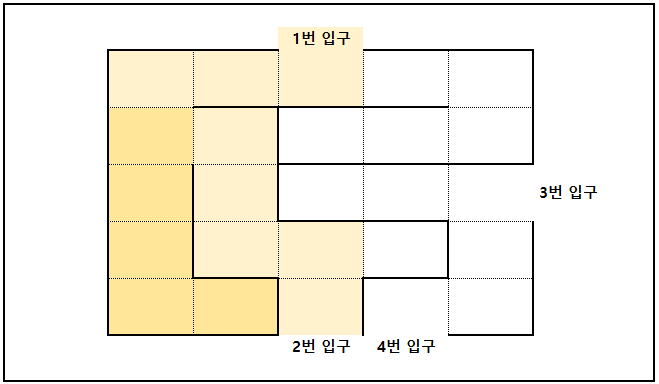
이걸 더 이상 이동할 수 있는 경우의 수가 없을 때 까지 반복한다.
각 칸에 있는 숫자는 중복해서 지나간 곳임을 표시했다.

이제 시작 지점을 선택했을 때, 그 지점과 연결된 탈출구가 몇 개가 있는지 한 번에 확인할 수 있다. 그렇지?
쉽게 말해서 막힐 때까지 한 길만 쭉 파는 거다. 경우의 수가 존재하지 않을 때까지.
"일반적으로 접근할 수 있는 길을 모두 탐색하는 것"
"그래프 계의 완전탐색"
그것이 DFS다.
2-2. DFS 이해 예시 #2
음... 아직도 모르겠거나 헷갈리면..
전형적인 그래프를 통해 알려주겠다.
아래와 같은 트리형 그래프가 있다고 해 보자.

하나의 길만 쭉 파는 형식으로 각 노드에 접근하면, 아래 사진 순서와 같이 이루어지게 될 것이다.
각 노드 안에 쓰여 있는 숫자는 그 노드에 접근한 순서라고 이해하면 된다.

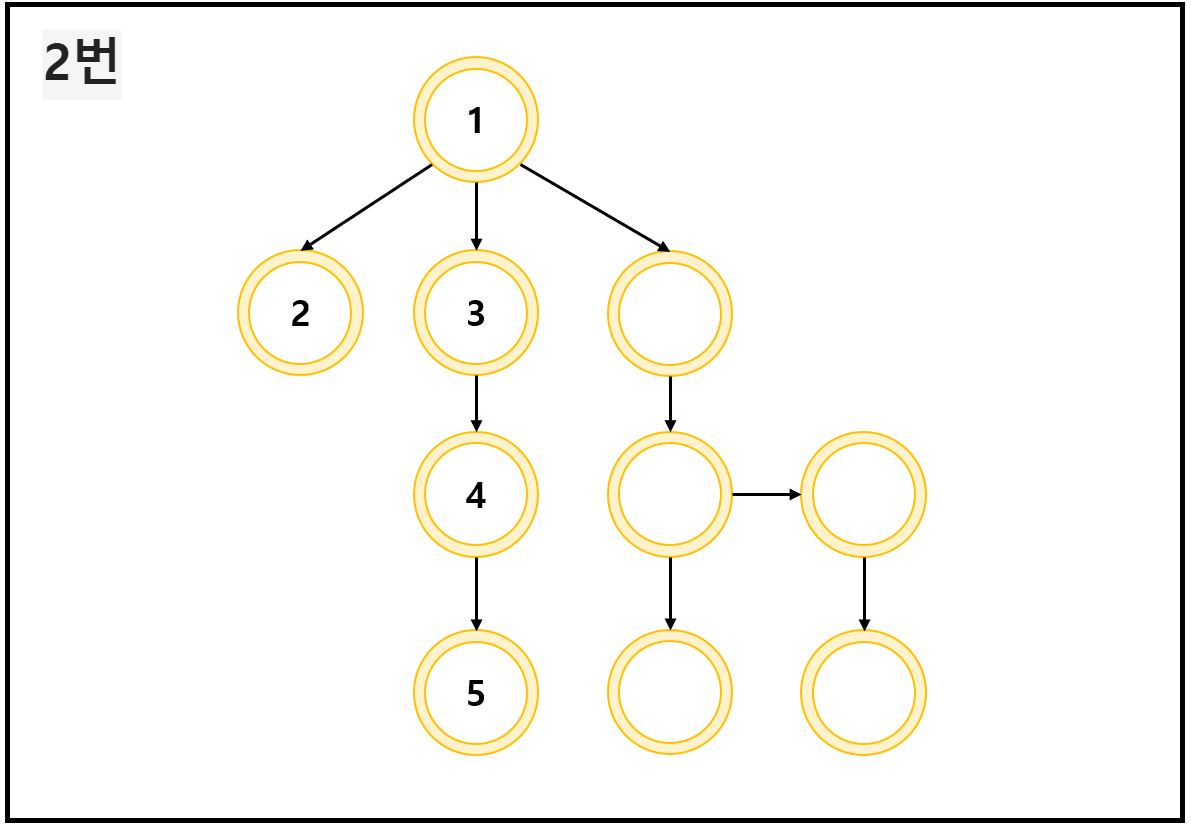
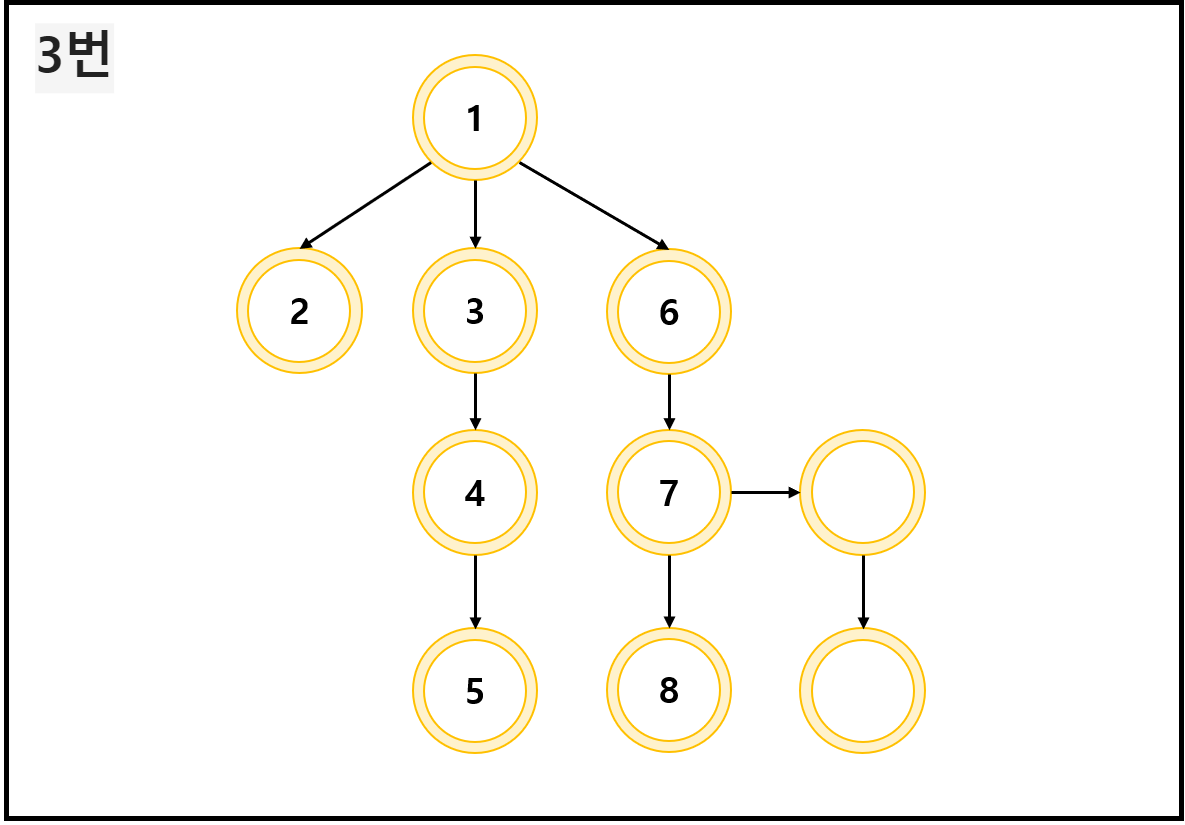
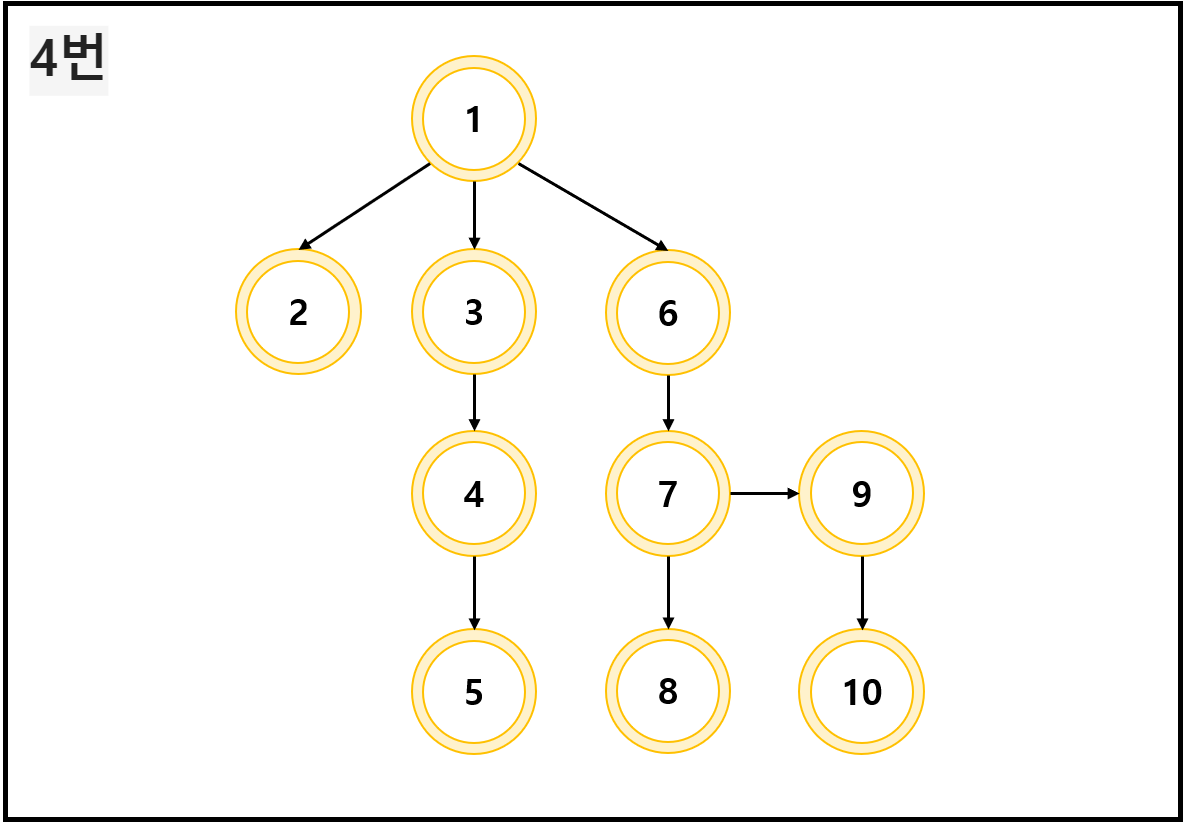
이 정도면... 이해가 되지 않았을까 싶다.
어느 정도 공부를 한 사람이라면, 위 플로우를 봤을 때
아! 재귀를 쓰면 되겠구나!
라고 느낄 수 있을 것이다! 모든 경우를 확인해야 하니까~
이제 실전과 함께 이해를 해 보도록 하자!
3. DFS 기본 문제 풀이
3-1. 문제 개요 확인
코드 트리(Codetree)에 좋은 문제가 하나 있더라.

자, 중요한 점만 짚어보면
문제 ❗
N개의 정점, M개의 간선이 입력 인자로 들어온다.1번 정점에서 이동을 시작했을 때 도달할 수 있는 정점 수는 몇 개인지를 출력한다. (노드 1번 제외)
천천히 한 스탭씩 풀어보자.
입출력 형식은 아래와 같다.

그리고, 본 글에서 서술할 때는 아래의 입출력 예제를 사용하겠다.

3-2. N, M 저장 및 2차원 배열 생성
우선 정점과 간선을 저장하는 2차원 배열이 필요하다.
해당 정점이 어디와 연결되어있는지를 저장하는 배열이 1차원 배열이고,
그러한 1차원 배열을 모아 놓은 것이 2차원 배열이 되도록 구현을 해 보자.
연결되어 있는 것은 "1", 연결되어있지 않으면 0으로 설정하겠다.

C++에서 Vector를 통해 선언을 해줄 것이다.
대충 간단하게 선언해 주자.
아래 코드를 통해 입력의 첫 번째 줄인 N과 M을 저장하고, 그에 맞춘 2차원 배열 공간을 선언했다.
#include <iostream>
#include <vector>
using namespace std;
int main() {
int N, M;
cin >> N >> M;
vector<vector<int>> graph(N, vector<int>(N, 0));
return 0;
}
3-2. 배열 내 정점 데이터 입력
자, 그럼 이제 배열에 값을 입력해 주자.
만약 입력이 "1 2"로 들어온다면 1번과 2번 정점에서 서로 연결되어 있다고 표시해 주어야 한다.
아래 코드에서 각 아이템에 -1을 하는 이유는, 입력하는 값이 1부터 시작하여 들어오기 때문이다.
for (int i = 0; i < M; i++)
{
int x, y;
cin >> x >> y;
graph[x-1][y-1] = 1;
graph[y-1][x-1] = 1;
}
예제 입력을 보면
{1 2} / {1 3} / {2 3} / {4 5} 이렇게 들어왔다.
자, 선언했던 2차원 배열에 데이터를 넣으면 아래와 같이 나오게 될 것이다.
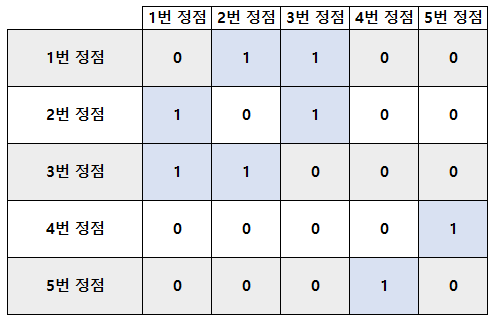
3-3. 무한 루프 예외처리
자, 그럼 이제 우리는 이 데이터를 기반으로 재귀를 돌려야 한다.
왜냐?
처음 DFS를 말할 때
"막힐 때까지 계속 진행한다"라고 했지 않는가.
1번 정점과 2번 정점을 예로 들어보자. 가장 먼저 만나는 길로 진행할 것이다.

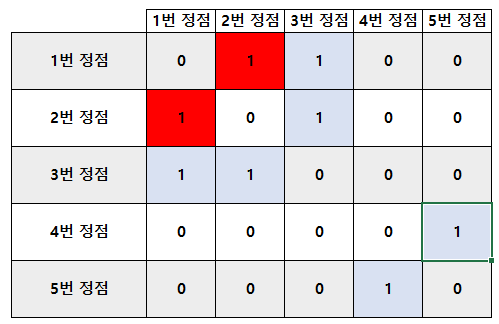
어라!
1번 정점에서 연결되었다고 해서 2번 정점으로 이동했는데,
2번 정점에서 처음 만나는 연결점이 1번 정점이라고 한다!
위처럼 진행하면
다시 1번 정점 이동 -> 2번 정점 이동 -> 1번정점 이동 -> 2번정점 이동...
이처럼 무한 반복이 되어버린다.
하여 "이미 지나갔던 정점"을 체크할 필요가 있다.
이것도 VECTOR STL로 bool 형 배열을 선언하여 관리해 주도록 할 것이다!
vector<bool> visit;
...
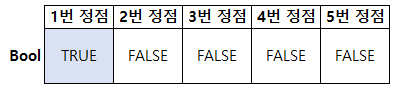
visit.resize(N, false);
visit[0] = true;
...
자, 왜 visit [0]은 미리 True로 설정을 하는지 궁금할 수 있다.
처음 문제에서 "1번 정점"에서 시작한다고 했고, 중복되는 건 처리하지 않기로 했지 않는가?
무한 반복과 중복 이동을 막기 위해 visit [0]을 미리 막아놓고 시작하는 거다.
3-4. DFS 설계 및 재귀 함수 구현
자,, 그럼 설계를 해보자.
정상적으로 실행된다면, 아래와 같은 순서로 실행되게 될 것이다.
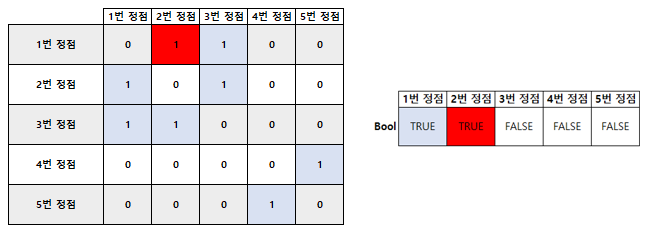


눈으로 봤으니, 이제 코드로 구현을 해 보자.
코드에서 구현해야 할 사항은 아래와 같이 될 것이다.
- 각 정점의 아이템이 1인지 검사한다
- 아이템이 1이라면, 해당 visit이 FALSE인지 검사한다
- 만약 visit도 FALSE라면 방문 정점으로 체크(TRUE)하고, 해당 정점을 기준으로 위 과정을 반복한다.
- 만약 visit이 TRUE라면 해당 아이템을 건너뛴다.
int result = 0;
void DFS(int target, const vector<vector<int>> &gp)
{
for (int i = 0; i < gp.size(); i++) // 정점 별 아이템 반복
{
if (gp[target][i] == 1 && !visit[i]) // 해당 아이템이 1이고, visit하지 않았는지 검사
{
result++; // 방문한 정점 개수 관리!
visit[i] = true; // visit 한 정점이라 표시
DFS(i, gp); // 해당 정점도 동일하게 동작하도록 설정
}
}
}
인자로 들어가는 "Target"은 점검하고자 하는 정점 번호가 될 것이고,
gp는 한참 전에 만들었던 2차원 배열인 그래프 데이터가 될 것이다.
여기서 왜 포인터로 만들었는지는... 메모리 관리에 대해 배워야 알 수 있는데, 간단하게 말하자면
2차원 배열을 수십 수백 개가 만들어지는 것을 방지하기 위함이다. << 이거 좀 중요하다. 알고리즘 풀이에선..
3-5. 실행 결과
DFS() 함수를 실행하고 난 뒤,
전역 변수로 선언한 result를 출력해 주기만 하면 이제 정답! 처리가 될 것이다.

코드 전문은 아래 접은 글을 펼쳐보자.
그래도! 열기 전에 스스로 짜 보는 것을 추천한다!!
codetree-TILs/240718/그래프 탐색 at main · devbini/codetree-TILs
TILs for codetree(https://www.codetree.ai). Contribute to devbini/codetree-TILs development by creating an account on GitHub.
github.com
#include <iostream>
#include <vector>
using namespace std;
vector<bool> visit;
int result = 0;
void DFS(int target, const vector<vector<int>> &gp)
{
for (int i = 0; i < gp.size(); i++)
{
if (gp[target][i] == 1 && !visit[i])
{
result++;
visit[i] = true;
DFS(i, gp);
}
}
}
int main() {
int N, M;
cin >> N >> M;
vector<vector<int>> graph(N, vector<int>(N, 0));
visit.resize(N, false);
for (int i = 0; i < M; i++)
{
int x, y;
cin >> x >> y;
graph[x-1][y-1] = 1;
graph[y-1][x-1] = 1;
}
visit[0] = true;
DFS(0, graph);
cout << result;
return 0;
}
4. 마치며
중간에 vector 배열 데이터를 포인터로 넘기는 부분이 있는데,
사실 필자가 그거 때문에 시간초과가 나와서 문제를 틀렸었다.

프로그램을 짤 때는 알고리즘도 알고리즘이지만,
그 외적인 메모리 관리는 기본적으로 할 수 있어야 한다.
자잘 자잘한 것들에서 코드의 가독성과 효율성, 메모리와 시간 복잡도가 크게 바뀔 수 있다는 것을 여러분들은 아셨으면 좋겠네요.

다음부터는 좀 더 신경 쓰고, 조심하도록 합시다!
다들 긴 글 읽고 공부하느라 고생하셨습니다.
다음 글에서 만나요!

'Algorithm' 카테고리의 다른 글
| [코드트리 조별과제] Memoization? 메모이제이션이란? (3) | 2024.08.03 |
|---|


댓글 개